publications

2026

1. 

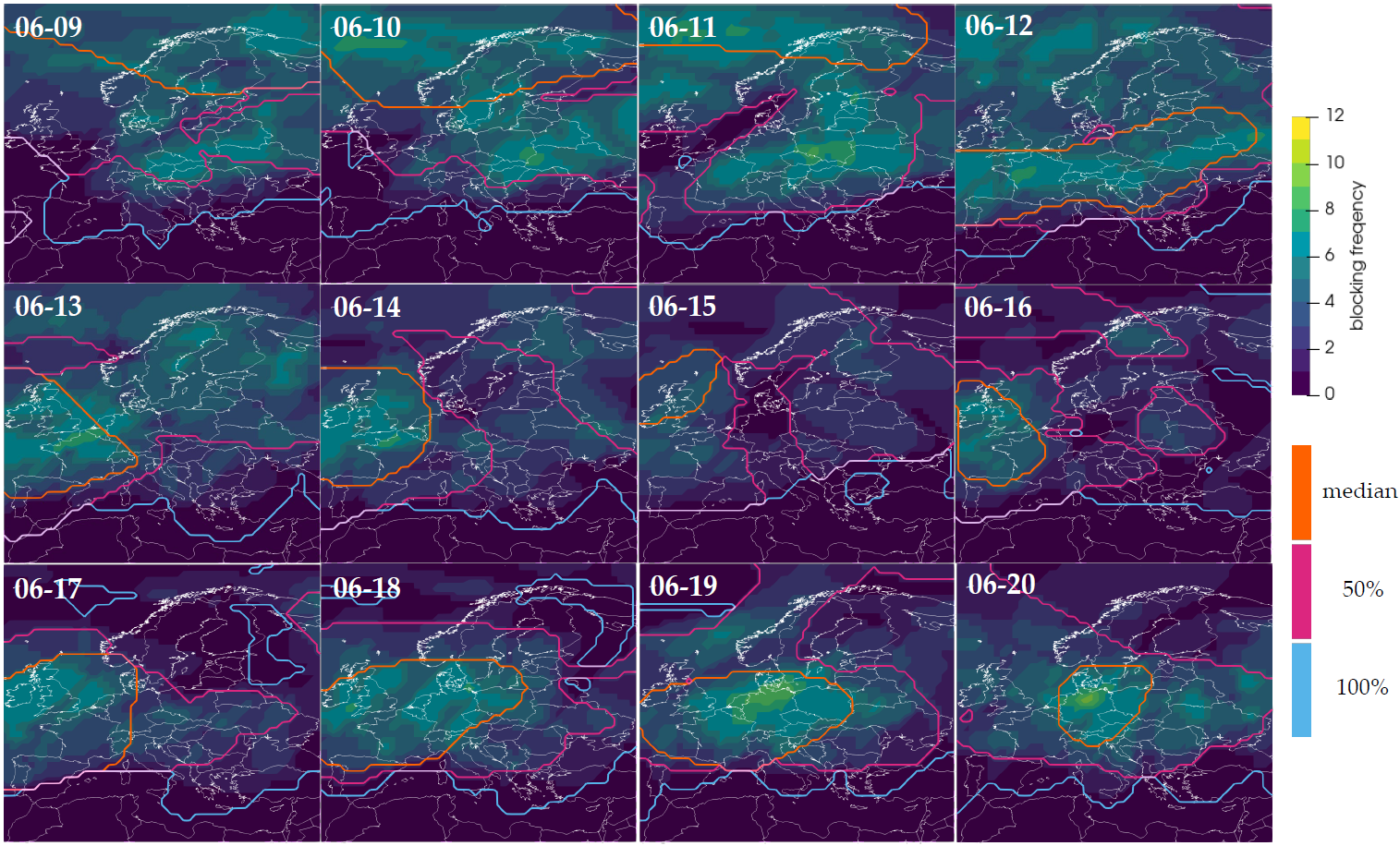   Spatiotemporal Detection and Uncertainty Visualization of Atmospheric Blocking Events

   Mingzhe Li, Peer Nowack, and Bei Wang

   IEEE Transactions on Visualization and Computer Graphics (PacificVis 2026 TVCG Journal Track), 2026

   accepted

   Abs PDF

   Atmospheric blocking events are quasi-stationary high-pressure systems that disrupt the typical paths of polar and subtropical air currents, often producing prolonged extreme weather events such as summer heat waves or winter cold spells. Despite their critical role in shaping mid-latitude weather, accurately modeling and analyzing blocking events in long meteorological records remains a significant challenge. To address this challenge, we present an uncertainty visualization framework for detecting and characterizing atmospheric blocking events. First, we introduce a geometry-based detection and tracking method, evaluated on both pre-industrial climate model simulations (UKESM) and reanalysis data (ERA5), which represent historical Earth observations assimilated from satellite and station measurements onto regular numerical grids using weather models. Second, we propose a suite of uncertainty-aware summaries: contour boxplots that capture representative boundaries and their variability, frequency heatmaps that encode occurrences, and 3D temporal stacks that situate these patterns in time. Third, we demonstrate our framework in a case study of the 2003 European heatwave, mapping the spatiotemporal occurrences of blocking events using these summaries. Collectively, these uncertainty visualizations reveal where blocking events are most likely to occur and how their spatial footprints evolve over time. We envision our framework as a valuable tool for climate scientists and meteorologists: by analyzing how blocking frequency, duration, and intensity vary across regions and climate scenarios, it supports both the study of historical blocking events and the assessment of scenario-dependent climate risks associated with changes in extreme weather linked to blocking.

2025

1. 

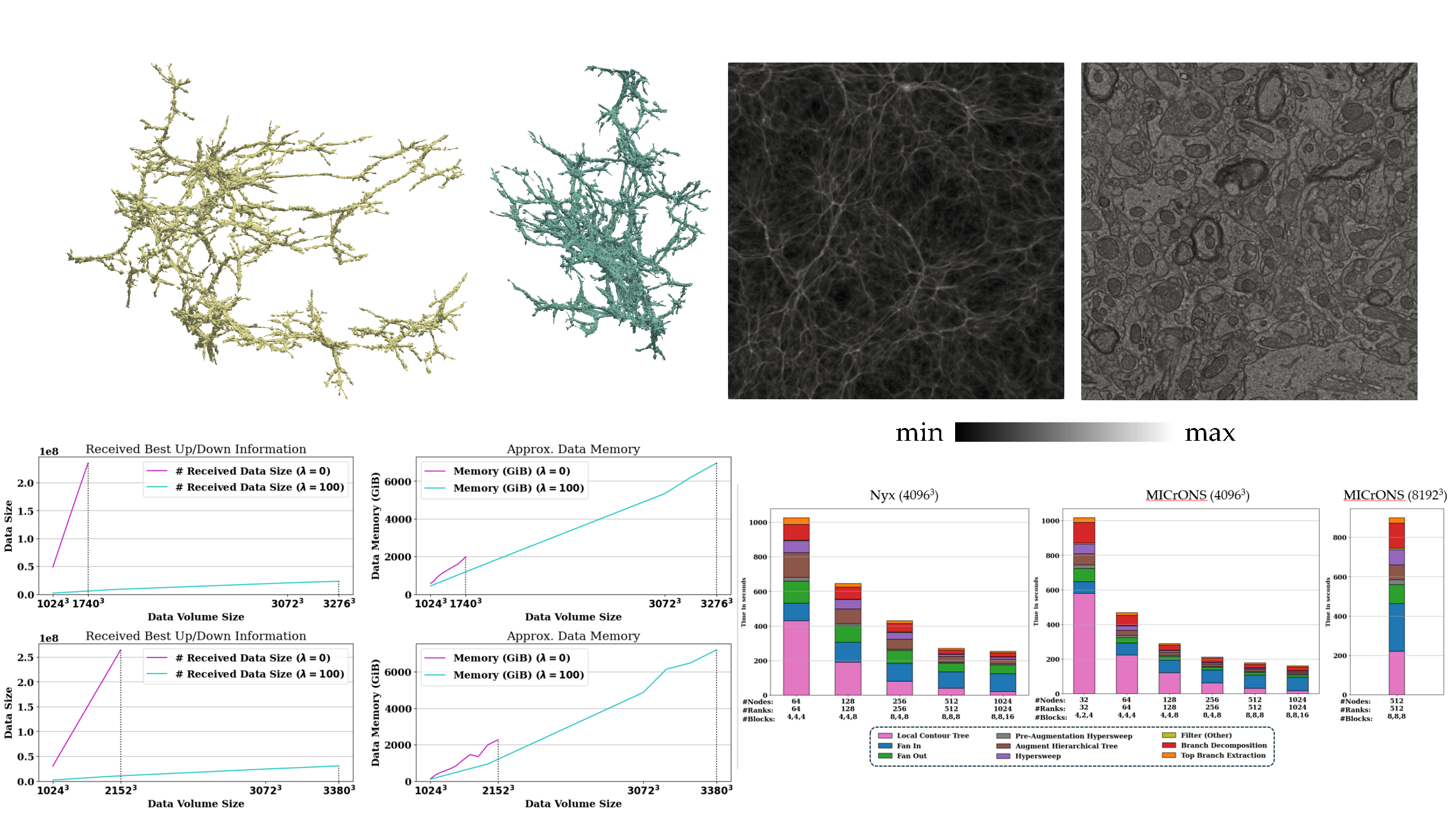   Extremely Scalable Distributed Computation of Contour Trees via Pre-Simplification

   Mingzhe Li, Hamish Carr, Oliver Rübel, and 2 more authors

   In 2025 The 15th IEEE Workshop on Large Data Analysis and Visualization (LDAV), 2025

   Abs PDF

   Contour trees offer an abstract representation of the level set topology in scalar fields and are widely used in topological data analysis and visualization. However, applying contour trees to large-scale scientific datasets remains challenging due to scalability limitations. Recent developments in distributed hierarchical contour trees have addressed these challenges by enabling scalable computation across distributed systems. Building on these structures, advanced analytical tasks—such as volumetric branch decomposition and contour extraction—have been introduced to facilitate large-scale scientific analysis. Despite these advancements, such analytical tasks substantially increase memory usage, which hampers scalability. In this paper, we propose a pre-simplification strategy to significantly reduce the memory overhead associated with analytical tasks on distributed hierarchical contour trees. We demonstrate enhanced scalability through strong scaling experiments, constructing the largest known contour tree—comprising over half a trillion nodes with complex topology—in under 15 minutes on a dataset containing 550 billion elements.

2. 

   Tracking Low-Level Cloud Systems with Topology

   Mingzhe Li, Dwaipayan Chatterjee, Franziska Glassmeier, and 2 more authors

   In 2025 Topological Data Analysis and Visualization (TopoInVis), 2025

   Abs PDF

   Low-level clouds are ubiquitous in Earth’s atmosphere, playing a crucial role in transporting heat, moisture, and momentum across the planet. Their evolution and interaction with other atmospheric components, such as aerosols, are essential to understanding the climate system and its sensitivity to anthropogenic influences. Advanced high-resolution geostationary satellites now resolve cloud systems with greater accuracy, establishing cloud tracking as a vital research area for studying their spatiotemporal dynamics. It enables disentangling advective and convective components driving cloud evolution. This, in turn, provides deeper insights into the structure and lifecycle of low-level cloud systems and the atmospheric processes they govern. In this paper, we propose a novel framework for tracking cloud systems using topology-driven techniques based on optimal transport. We first obtain a set of anchor points for the cloud systems based on the merge tree of the cloud optical depth field. We then apply topology-driven probabilistic feature tracking of these anchor points to guide the tracking of cloud systems. We demonstrate the utility of our framework by tracking clouds over the ocean and land to test for systematic differences in the two physically distinct settings. We further evaluate our framework through case studies and statistical analyses, comparing it against two leading cloud tracking tools and two topology-based general-purpose tracking tools. The results demonstrate that incorporating system-based tracking improves the ability to capture the evolution of low-level clouds. Our framework paves the way for detailed low-level cloud characterization studies using satellite data records.

3. 

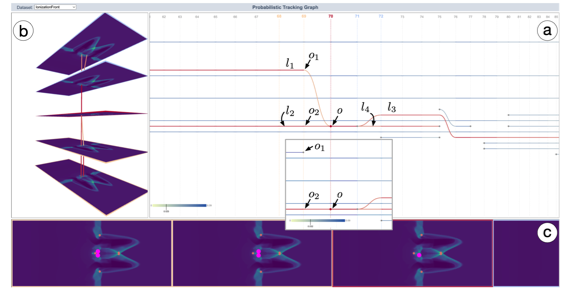   Flexible and Probabilistic Topology Tracking with Partial Optimal Transport

   Mingzhe Li, Xinyuan Yan, Lin Yan, and 2 more authors

   IEEE Transactions on Visualization and Computer Graphics, 2025

   Abs PDF

   In this paper, we present a flexible and probabilistic framework for tracking topological features in time-varying scalar fields using merge trees and partial optimal transport. Merge trees are topological descriptors that record the evolution of connected components in the sublevel sets of scalar fields. We present a new technique for modeling and comparing merge trees using tools from partial optimal transport. In particular, we model a merge tree as a measure network, that is, a network equipped with a probability distribution, and define a notion of distance on the space of merge trees inspired by partial optimal transport. Such a distance offers a new and flexible perspective for encoding intrinsic and extrinsic information in the comparative measures of merge trees. More importantly, it gives rise to a partial matching between topological features in time-varying data, thus enabling flexible topology tracking for scientific simulations. Furthermore, such partial matching may be interpreted as probabilistic coupling between features at adjacent time steps, which gives rise to probabilistic tracking graphs. We derive a stability result for our distance and provide numerous experiments indicating the efficacy of our framework in extracting meaningful feature tracks.

4. 

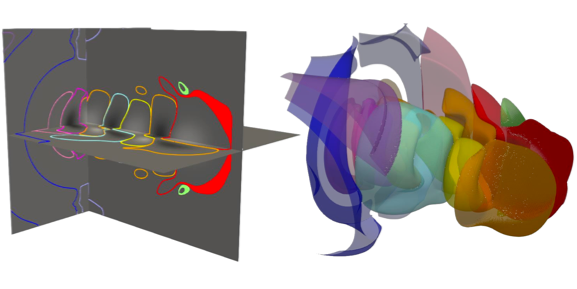   Distributed Augmentation, Hypersweeps, and Branch Decomposition of Contour Trees for Scientific Exploration

   Mingzhe Li, Hamish Carr, Oliver Rübel, and 2 more authors

   IEEE Transactions on Visualization and Computer Graphics (VIS 2024 Full Paper), 2025

   Abs PDF

   Contour trees describe the topology of level sets in scalar fields and are widely used in topological data analysis and visualization. A main challenge of utilizing contour trees for large-scale scientific data is their computation at scale using highperformance computing. To address this challenge, recent work has introduced distributed hierarchical contour trees for distributed computation and storage of contour trees. However, effective use of these distributed structures in analysis and visualization requires subsequent computation of geometric properties and branch decomposition to support contour extraction and exploration. In this work, we introduce distributed algorithms for augmentation, hypersweeps, and branch decomposition that enable parallel computation of geometric properties, and support the use of distributed contour trees as query structures for scientific exploration. We evaluate the parallel performance of these algorithms and apply them to identify and extract important contours for scientific visualization.

2023

1. 

   Comparing Morse Complexes Using Optimal Transport: An Experimental Study

   Mingzhe Li, Carson Storm, Austin Yang Li, and 2 more authors

   In 2023 IEEE Visualization and Visual Analytics (VIS), 2023

   Abs PDF

   Morse complexes and Morse-Smale complexes are topological descriptors popular in topology-based visualization. Comparing these complexes plays an important role in their applications in feature correspondences, feature tracking, symmetry detection, and uncertainty visualization. Leveraging recent advances in optimal transport, we apply a class of optimal transport distances to the comparative analysis of Morse complexes. Contrasting with existing comparative measures, such distances are easy and efficient to compute, and naturally provide structural matching between Morse complexes. We perform an experimental study involving scientific simulation datasets and discuss the effectiveness of these distances as comparative measures for Morse complexes. We also provide an initial guideline for choosing the optimal transport distances under various data assumptions.

2. 

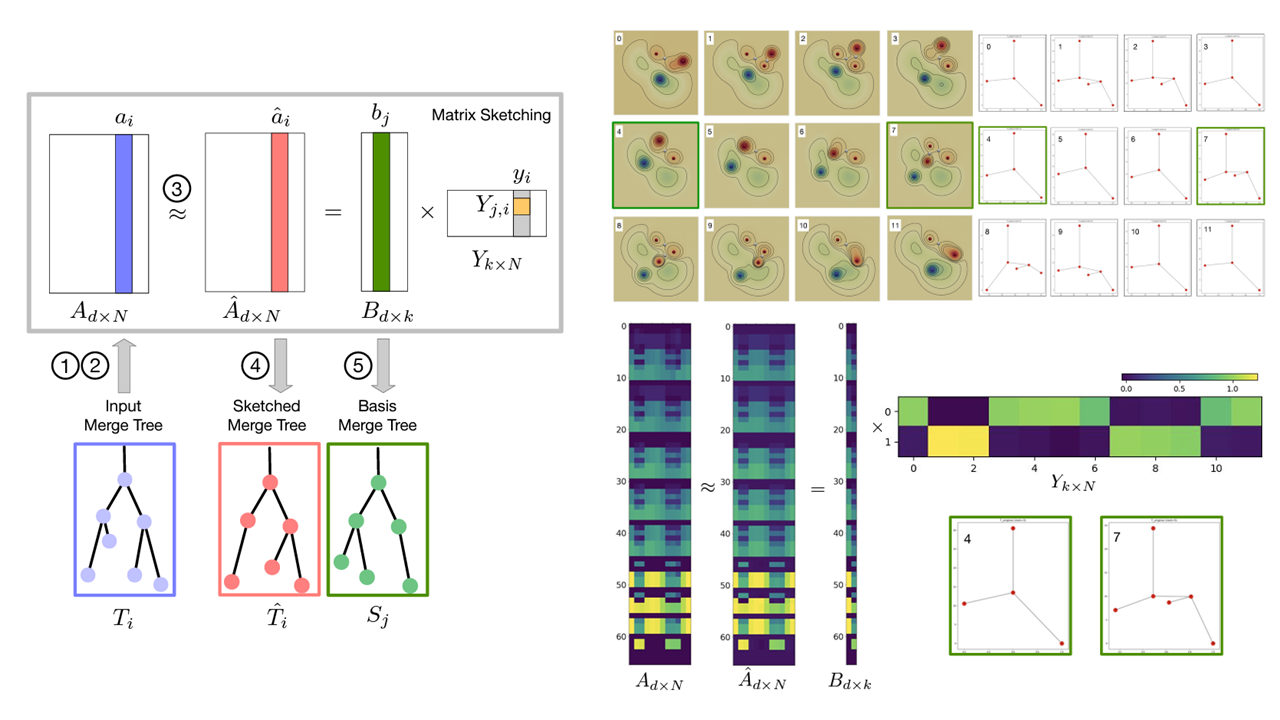
   Sketching Merge Trees for Scientific Visualization

   Mingzhe Li, Sourabh Palande, Lin Yan, and 1 more author

   In 2023 Topological Data Analysis and Visualization (TopoInVis), 2023

   Abs PDF

   Merge trees are a type of topological descriptors that record the connectivity among the sublevel sets of scalar fields. They are among the most widely used topological tools in visualization. In this paper, we are interested in sketching a set of merge trees using techniques from matrix sketching. That is, given a large set T of merge trees, we would like to find a much smaller set of basis trees S such that each tree in T can be approximately reconstructed from a linear combination of merge trees in S. A set of high-dimensional vectors can be approximated via matrix sketching techniques such as principal component analysis and column subset selection. However, until now, there has not been any work on sketching a set of merge trees. We develop a framework for sketching a set of merge trees that combines matrix sketching with tools from optimal transport. In particular, we vectorize a set of merge trees into high-dimensional vectors while preserving their structures and structural relations. We demonstrate the applications of our framework in sketching merge trees that arise from time-varying scientific simulations. Specifically, our framework obtains a set of basis trees as representatives that capture the “modes” of physical phenomena for downstream analysis and visualization.